A Probabilistic Approach to Distributed Clock Synchronization

One-line summary: Provable, low bounds on clock synchronization precisions are easily obtained with a relatively simply protocol and trivial computation.

Overview/Main Points

• Fundamentals: The fundamental protocol is for a process P to send a query message to process Q; process Q replies to P with a message containing Q's clock time at the instant Q received P's message. We assume hardware clocks have drift rate 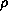, implying the measurement of a time interval t'-t has an error of at most 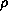(t-t'). Assume further that the minimum message transmission delay between P and Q is min.
• Clock synch and max error: It is proven in the paper that if P measures the round-trip time of the request/reply pair as 2D, the value displayed by Q's clock when it sends its reply is T, and the value displayed by Q's clock when P receives this reply is 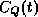, then the best guess by P for 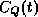is:
  with maximum error
  .
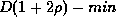• Obtaining a desired precision: The precision of the clock estimate is limited by the measured round-trip time of the reply/request pair. By timing out any requests that don't receive replies within 2U seconds, one can bound the imprecision of a given clock (at the risk of requiring one to resend a clock resynchronization request) to be e by by choosing a U of: 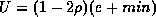. 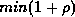Because the minimum U one can pick is (because of the minimum delivery latency plus clock drift), the best precision achievable by this method is .
• Maintaining a desired precision: Because the local clock drifts, it must be resynchonized periodically to maintain a desired precision. Because delivery latency is potentially unbounded, one must set a reply/request timeout, which implies a resynchronization request could fail. One can calculate the probability of N successive request failures; given a current precision, and a specifiable probability of success and a specifiable desired precision, one can calculate the delay between the periodic resynchronization attempts.
• Detecting failures: Hard bounds on possible imprecisions are provable with this scheme. If a calculated clock time falls outside of those bounds, a clock failure (at the master or at the slave) has occured. Because a master has a reliable clock source, the master can detect if its own clock as failed, and since masters update themselves more frequently than slaves, a slave can deduce its own clock has failed if such an erroneous condition occurs two times in a row without the master declaring itself invalid.

Relevance

Flaws

• The only flaw of this paper is that the extremely rigorous presentation belies the fact that if any of the assumptions are violated, then all certainty flies out the window.