CS121
Introduction to Artificial Intelligence
Winter 2004
Homework #3
(Search Problems)
Out:
How to complete this HW: First copy this
file; then insert your answers in the file immediately below each question;
finally submit the completed file to the submission webpage https://www.stanford.edu/class/cs121/hwsub/hw3.fft
before 2/4 at
Note on Honor Code: You must NOT look at previously published solutions of any of these problems in preparing your answers. You may discuss these problems with other students in the class (in fact, you are encouraged to do so) and/or look into other documents (books, web sites), with the exception of published solutions, without taking any written or electronic notes. If you have discussed any of the problems with other students, indicate their name(s) here:
Any intentional transgression of these rules will be considered an honor code violation.
General information: In the following, whenever an explanation is required (Why?), there will not be full-credit without an explanation. Keep explanations short and to the point. Excessive verbosity will be penalized. If you have any doubt on how to interpret a question, either tell us in advance, so that we can help you understand the question, or tell us how you understand it in your returned solution.
Grading:
|
Problem# |
Max. grade |
Your grade |
|
I |
5 |
|
|
II |
10 |
|
|
III |
10 |
|
|
IV |
15 |
|
|
Total |
10 |
|
Express the problem of finding a suitable ordering as a CSP. Clearly state your variables and constraints.
II. (10 points) Consider the
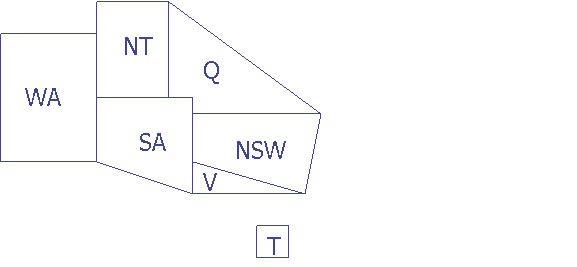
The constraint satisfaction problem consists of 7 variables {WA,NT,SA,Q,NSW,V,T}. Each variable has the same domain {red, green, blue}. No two adjacent variables have the same value, so the constraints are: WAΉNT, WAΉSA, NTΉSA, NTΉQ, SAΉQ, SAΉNSW, SAΉV,QΉNSW, NSWΉV.
- Determine the total number of distinct color assignments, valid and invalid, in this map-coloring problem.
2. Using backtracking, forward checking, and the following heuristics:
· Most-constrained variable
· Most-constraining variable
· Least-constraining value
count
how many of them are valid.
III. (10 points) The following:
S E N D
+ M O R E
--------------
M O N E Y
is a cryptarithmetic problem. Each letter must be given a digit value (0 through 9), with M ≠ 0. No two letters must have the same value. The sum of the digits must be as shown in the problem. The solution of the above problem is:
D = 7, E = 5, M = 1, N = 6, O = 0, R = 8, S = 9, Y =2.
Indeed:
9 5 6 7
+ 1 0 8 5
------------
1 0 6 5 2
Another example is:
C R O S S
+ R O A D S
----------------
D A N G E R
with D Ή 0.
1. Express this second problem as a constraint satisfaction problem: what are the variables, their possible values, the constraints? (Express the constraints in algebraic language.) [Hint: In addition to the obvious variables, introduce the 5 carries as additional variables.]
2. Give a solution of the problem. In no more than 10 lines, sketch the techniques that allow you to compute this solution.
IV. (15 points) In the following map-coloring problem, each variable has the domain {red, green, blue}

Lets say we start out by coloring country A red.
1. What will the domains of B, C, and D be after doing forward checking? After AC3? (It is not necessary to show the full details of either algorithm; high-level explanations of why a value is removed from a particular variables domain is sufficient.)
2. Without instantiating any more variables, what further inconsistent values can you eliminate? Explain why forward checking and AC3 werent able to do this.
3. Formulate a constraint propagation algorithm specific to the map-coloring problem that will correctly detect the kind of inconsistency shown in part 2. Note that this algorithm does not need to duplicate the behavior of forward checking or AC3. Pseudo-code is not necessary, but your formulation should be precise.